一.事件

概率事件，必然事件，不可能事件

帽子分开戴，中间符号反过来

概率的概念与性质

P(A∪B∪C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)

二.古典概型

古典概型也叫等可能概型 用样本数估计概率

抽签原理 不放回摸出特定奖的概率不变

三.条件概率

乘法公式：对条件概率公式进行的变化，用来求P(AB)

四.全概率公式与贝叶斯公式

考试经常会出两个Bi仅有B和非B的简化版，如下

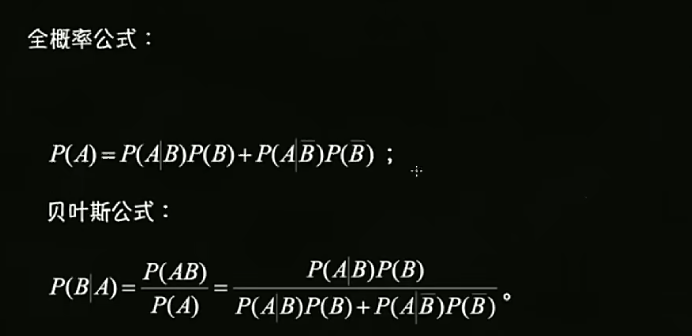
计算题第一题 10分

第一步 把事件假设出来

第二步 根据已知概率把假设的时间概率表示出来

第三步 用全概率公式计算某一个事件的概率**

第四步 用计算过的概率计算贝叶斯公式（当分母）**

五.事件的独立性

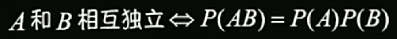
概率为0的事件未必是不可能事件

六.离散型随机变量及其分布

分布律x有n个取值，则分布函数后面就有n+1行

等号都在大于等于上面，第一条一定是0 最后一条一定是1

七.常见的离散型随机变量

二项分布，泊松分布

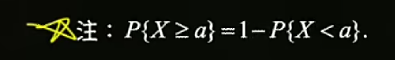
八.连续型随机变量及其分布

连续型随机变量单点概率为0：因为某一段上有无穷多个点

概率等于零的点未必为不可能事件

知道 分布函数F(x) 求 概率密度函数f(x) -> 求导

知道 概率密度函数f(x) 求 分布函数F(X) -> 求积分

知道x的分布函数与概率密度函数 求 y 的概率密度函数

1）确定y的取值

2）确定y的分布函数

3）求概率密度函数

九.常见的连续随机变量

十.二维离散型随机变量

十一.二维连续型随机变量

十二.二维随机变量函数的分布

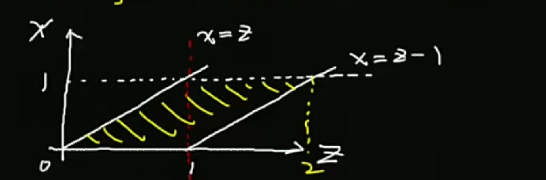
把x或者y用z和另一个变量替代再求积分

这时候要注意可能会出现积分线的不同，要分段求

x当纵坐标 z当横坐标

十三.期望与方差

数学期望：数学期望主要是描述数据大概分布的一个值，一个期望值

方差：描述样本和期望值的离散程度，一般方差越小说明预测效果越准确

数学期望

数学期望的性质

2,3,4条经常考到

方差和标准差

平方的期望-期望的平方

方差的性质

常见的期望和方差

正态分布：已知X，要求Y，只要算出Y的期望和方差，就能写出Y的正态分布函数

正态函数加减乘除一个常数依旧是正态分布

对谁求积分 就在哪条轴上划线

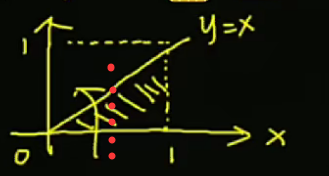
对x 求积分dx 即找出x的取值范围为0到y

十四.协方差与相关系数

如果X跟Y不相关，那么协方差等于0 Cov(X,Y)=0

相关系数描述了两个随机变量X,Y之间的依赖关系

如果越接近1说明越为正相关，越接近-1说明越为负相关 0说明无关

已知X,Y的方差，和二者的相关系数，可以求出x和y的协方差

十五.中心极限定理

一些随机变量的加和概率 并且 发现这些随机实验独立同分布->要运用中心极限定理计算

十六.抽样分布

常用统计量：g（x1,x2,x3,...,xn）这种不含位置参数的变量叫做常用统计量

常用分布

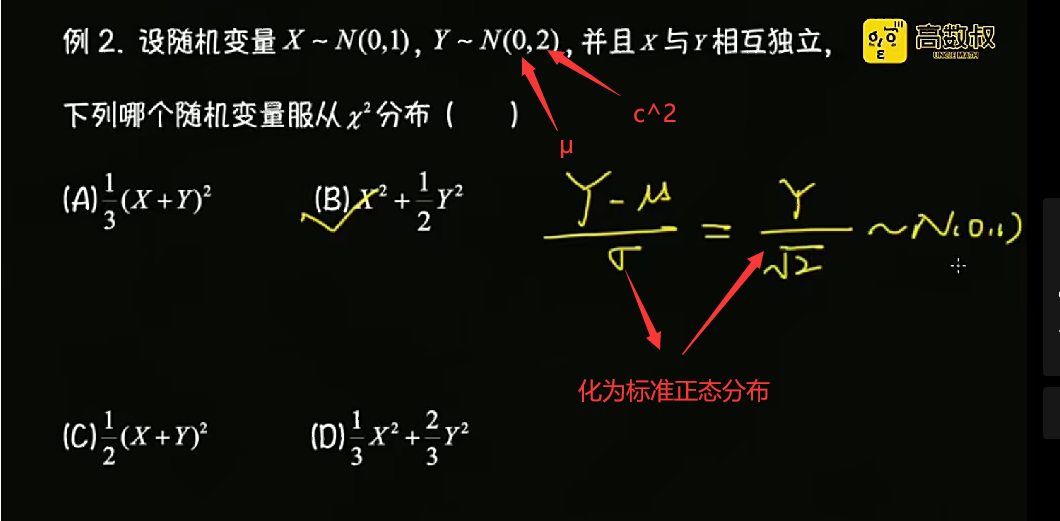
十七.矩估计

1.计算出一个总体均值的表达式

2.令总体均值等于样本均值，反解出未知参数关于样本均值的函数

3.求出样本均值，带入求估计值

十八.最大似然估计（离散型）

十九.最大似然估计（连续型）

二十.无偏估计